1.-
Una bailarina de ballet que pesa 50 kp está apoyada sobre la punta del pie. ¿Cuál es la presión sobre el área del suelo que toca, si la punta de su pie tiene un área de 22,7 cm2?
2.-
El filo de un cincel tiene un área de 0,12 pulg2. Cuando se golpea con un martillo, el cincel ejerce una fuerza momentánea de 20 lb sobre un ladrillo.
¿Cuál es la presión ejercida directamente debajo del filo del cincel?
3.-
Una explosión origina un aumento momentáneo en la presión del aire ambiente (sobrepresión). Calcular la fuerza total ejercida por una sobrepresión de 2758 N/m2 sobre la pared de un edificio de 6 m de alto y 9 m de ancho.
4.-
La presión sistólica de un paciente es 220 mm Hg. Convertir esta presión en
(a) pascales, (b) libras por pulgada cuadrada y (c) centímetros de agua.
5.-
La presión (manométrica) del aire suministrado a un paciente por medio de un respirador es 20 cm H20. Convertir esta presión en
(a) newtons por metro cuadrado,
(b) libras por pulgada cuadrada y
(c) torrs.
6.-
Los diámetros de los émbolos grande y pequeño de un elevador hidráulico (Fig. 7.6) son 6,0 y 1,5 pulg, respectivamente, (a) ¿Cuál es la fuerza que debe aplicarse al émbolo más pequeño para levantar un automóvil de 2000 Ib colocado sobre el émbolo grande? (b) Si el émbolo pequeño desciende 5 pulg, ¿cuánto sube el émbolo grande?
7.-
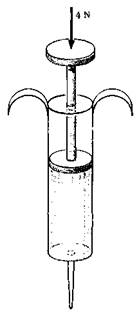Se aplica una fuerza de 4 N al émbolo de una jeringa hipodérmica cuya sección transversaltiene un área de 2,5 cm2.
(a) ¿Cuál es la presión (manométrica) en el fluido que está dentro de la jeringa?
(b) El fluido pasa a través de una aguja hipodérmica cuya sección transversal tiene un área de 0,008 cm2. ¿Qué fuerza habría de aplicarse al extremo de la aguja para evitar que el fluido saliera?
(c) ¿Cuál es la fuerza mínima que debe aplicarse al émbolo para inyectar fluido en una vena en la que la presión sanguínea es 12 mm Hg?
8.-
El corazón impulsa sangre a la aorta a una presión media de 100 mm Hg. Si el área de la sección transversal de la aorta es 3 cm2, ¿cuál es la fuerza media ejercida por el corazón sobre la sangre que entra en la aorta?
9.-
¿Cuál es la masa de 200 ml de triclorometano?
10.-
Calcular la masa del aire de una habitación de 6 m de ancho, 10 m de larga y 4 m de alta.
11.-
(a) Calcular la masa de un cilindro de aluminio de 10 cm de largo y 4 cm de diámetro.
(b) La masa de un cilindro de tungsteno del mismo tamaño y forma es 1758 g. ¿Cuál es la densidad del tungsteno?
12.-
Una pulgada de agua (pulg H20), unidad de presión utilizada a veces en terapia respiratoria, es la presión ejercida por una columna de agua de 1 pulg de alta. Hacer la conversión de pulgadas de agua a (a) centímetros de agua y (b) milímetros de mercurio.
13.-
La pulgada de mercurio es una unidad de presión que se emplea a veces en meteorología. Hacer la conversión de pulgadas de mercurio a (a) milímetros de mercurio y (b) atmósferas.
14.-
Un dique presenta un escape a 4 m por debajo de la superficie del agua. Si el área del agujero es 1,5 cm2, ¿cuál es la fuerza que debe aplicar un niño holandés al agujero para evitar que se salga el agua?
15.-
(a) Fluye plasma desde un frasco a través de un tubo hasta una vena del paciente. Cuando el frasco se mantiene a 1,5 m por encima del brazo del paciente, ¿cuál es la presión del plasma cuando penetra en la vena? (b) Si la presión sanguinea en la vena es 12 mm Hg, ¿cuál es la altura mínima a la que debe mantenerse el frasco para que el plasma fluya en la vena? (c) Supongamos que un astronauta necesita una transfusión en la Luna. ¿A qué altura mínima habría que mantener el frasco en este caso? En la Luna g es 1,63 m/s2
16.-
En un primitivo experimento para demostrar la existencia de la presión sanguínea, se hacía pasar la sangre de una arteria de un caballo hasta el fondo de un tubo vertical. ¿A qué altura subía la sangre en el tubo? Supóngase que la presión sanguínea del caballo es 80 mm Hg y que la densidad de la sangre del caballo es la misma que la de la sangre humana.
17.-
Algunas personas experimentan molestias de oído al subir en un ascensor a causa del cambio de presión. Si la presión detrás del tímpano no varía durante la subida, la disminución de la presión exterior da lugar a una fuerza neta sobre el tímpano dirigida hacia afuera,
(a) ¿Cuál es la variación en la presión del aire al subir 100 m en un ascensor?
(b) ¿Cuál es la fuerza neta sobre un tímpano de área 0,6 cm2?
18.-
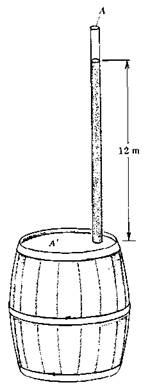Alrededor de 1646 Pascal llevó a cabo el experimento que se muestra en la figura. Se conectó un tubo muy largo, cuya sección transversal tenía un área A = 3 × 105 m2, a un barril de vino que tenía una tapa de área A' = 0,12 m2. Primero se llenó el barril de agua y a continuación se añadió agua al tubo hasta que el barril reventó. Esto sucedió cuando la columna de agua era de 12 m de alta. Precisamente antes de que el barril reventara, ¿cuál era ...
(a) el peso del agua contenida en el tubo,
(b) la presión (manométrica) del agua sobre la tapa del barril, (c) la fuerza neta ejercida sobre la tapa?
OBSERVACION. Obsérvese que el agua contenida en el tubo, aunque pesaba menos de 1 lb, era capaz de ejercer una fuerza de miles de libras sobre la tapa del barril.
19.-
Con un intenso esfuerzo de inspiración, por ejemplo, aspirando a fondo, la presión manométrica en los pulmones puede reducirse a —80 mm Hg.
(a) ¿Cuál es la altura máxima a la que puede ser sorbida el agua en una bombilla?
(b) La ginebra tiene una densidad de 920 kg/m3 ¿Cuál es la altura máxima a la que puede ser sorbida la ginebra en una bombilla?
20.-
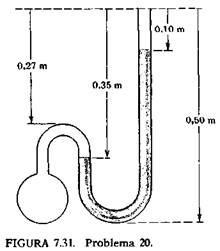Un manómetro de mercurio está conectado a una vasija del modo que se indica en la Figura.
(a) ¿Cuál es la presión (manométrica) en la vasija?
(b) ¿Cuál es la presión absoluta en la vasija, suponiendo que la presión atmosférica es 1,01×105 N/m2?
(c) Si se duplica la presión absoluta en la vasija, ¿cuál es la presión manométrica?
21.-
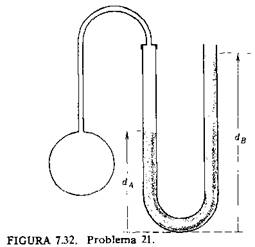Un manómetro de mercurio está conectado a una vasija tal como se representa en la figura.
(a) Si la altura dA de la columna de la izquierda es 0,22 m, ¿cuál es la altura dB de la columna de la derecha cuando la presión manométrica dentro de la vasija es 0,16×105 N/m2?
(b) ¿Cuáles son las alturas dA y dB cuando la presión manométrica es 0,32×105 N/m2?
22.-
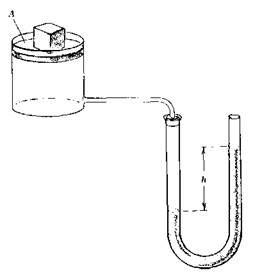Un cilindro cuya sección transversal tiene un área A = 4×104 m2 está conectado mediante un tubo a una de las ramas de un manómetro de mercurio . ¿Cuál es la diferencia de alturas en las dos
columnas cuando se coloca una masa de 3 kg sobre el émbolo del cilindro?
23.-
¿Qué altura habría de tener un barómetro llenado con glicerina?
24.-
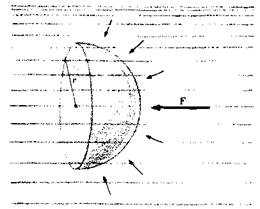Se sumerge un objeto hemisférico en un fluido. Demostrar que la fuerza total F sobre la porción curvada del hemisferio, es decir, el vector suma de las fuerzas que actúan sobre cada uno de los puntos de esta superficie, tiene el módulo F = πr2p, donde r es el radio de la esfera y p es la presión en el fluido.
(Indicación. Hallar primero la fuerza total sobre la superficie plana y utilizar luego la primera ley de Newton. No tener en cuenta las variaciones de la presión con la profundidad.)
25.-
En 1654 Otto von Guericke hizo una demostración en Magdeburgo del efecto de la presión del aire. Para desalojar el aire de entre dos hemisferios de metal hizo uso de una bomba de aire que él mismo había inventado. Tiros de ocho caballos, tirando de cada hemisferio, fueron después incapaces de separarlos. Si el radio de cada hemisferio era 0,3 m y la presión dentro de ellos 0,1 atm, ¿qué fuerza habría tenido que ejercer cada tiro de caballos para separar los hemisferios? (Usar el resultado del Prob. 24.)
26.-
¿Qué fracción de un iceberg queda por debajo de la superficie del agua?
27.-
Una «burbuja» de aire caliente (30 °C), formada cerca del suelo, asciende en el aire frío (10ºC) situado encima del suelo.
(a) Si el volumen de la burbuja es 8 m3 ¿cuál es la fuerza total sobre ella?
(b) ¿Cuál es la aceleración ascendente de la burbuja si se desprecia la resistencia del aire?
28.-
¿Cuál es la aceleración ascendente de un bloque de madera que se suelta en el fondo de un lago?
29.-
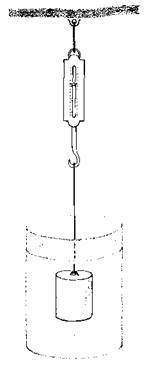Un bloque de aluminio de 2 kg está en el agua colgado de una cuerda unida a una balanza.
¿Cuál es la indicación de la balanza?
30.-
Cuando un peso W colgado de una cuerda unida a una balanza se sumerge en el agua (Figura anterior), la balanza marca W'. Demostrar que la densidad ρ del objeto colgado es ...
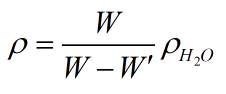
donde ρ H2O es la densidad del agua.
31.-
La velocidad vm de la sangre en el centro de un capilar es 0,066 cm/s. La longitud L del capilar es 0,1 cm y su radio r es 2 × 10 -4 cm.
(a) ¿Cuál es el flujo Q en el capilar?
(b) Hacer un cálculo aproximado del número total de capilares del cuerpo a partir del hecho de que el flujo a través de la aorta es 83 cm3/s.
32.-
(a) Calcular la resistencia que presenta a la sangre el capilar descrito en el Prob. 31.
(b) Calcular la resistencia cuando el radio del capilar se dilata hasta 2,5 × 10 -4 cm.
33.-
(a) ¿Cuál es la resistencia al agua de un capilar de vidrio de 20 cm de longitud y 0,06 cm de radio?
(b) ¿Cuál es el flujo a través del capilar cuando la diferencia de presión entre sus extremos es 15 cm H2O?
(c) ¿Qué diferencia de presión da un flujo de 0,5 cm3/s?
34.-
(a) ¿Cuál es la resistencia al agua de una aguja hipodérmica de 8 cm de longitud y 0,04 cm de radio interno?
(b) La aguja está unida a una jeringa con un émbolo de 3,5 cm2 de área. ¿Cuál es la fuerza que debe aplicarse al émbolo para conseguir que el agua fluya de la jeringa a una vena con una velocidad de flujo de Q = 2 cm3/s?
Supóngase que la presión en la vena es 9 mm Hg.
35.-
Durante la micción, la orina fluye desde la vejiga, donde su presión manométrica es 40 mm Hg, a través de la uretra hasta el exterior. Calcular el diámetro de una uretra femenina si se conocen los siguientes datos:
Longitud de la uretra femenina = 4 cm.
Flujo durante la micción = 21 cm3/s.
Viscosidad de la orina = 6,9 × 10-4 Pl.
37.-
Se ha hallado experimentalmente que el flujo de un fluido de densidad ρ y viscosidad η a través de una tubería de radio r es laminar mientras el numero de Reynolds
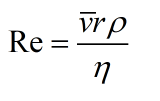
es menor que 1000. Aquí v es la velocidad media del fluido en la tubería. A partir de los datos de las tablas de densidad y vioscosidad, calcular el número de Reynolds para el flujo de sangre
(a) a través de la aorta y
(b) a través de un capilar típico.
39.-
Un fluido ejerce una fuerza viscosa Fv sobre un objeto que se desplaza a través de él. Para una pequeña esfera de radio r que se mueve lentamente con velocidad v, la fuerza viene dada por la ley de Stokes
Fv = 6π η r v
(a) ¿Cuál es la fuerza viscosa sobre una gotita de agua de radio r = 0,02 cm que se mueve en el aire con la velocidad v =2 m/s?
(b) Una gotita que cae aumenta su velocidad hasta que la fuerza viscosa equilibra el peso de la gotita. A partir de aquí la gotita cae a velocidad constante vf, llamada velocidad límite. Demostrar que la velocidad límite viene dada por
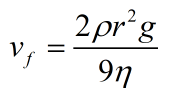
donde ρ es la densidad de la gotita y η es la viscosidad del aire,
(c) ¿Cuál es la velocidad límite de la gotita en el caso (a)?